27. Load
combination with the seismic actions
The structural behaviour of the bridge
under the seismic actions has been studied taking into account the
non-linear behaviour of the masonry, as it was done for the flood force.
A very reliable seismic analysis can be
performed using the step by step procedure, which is also well suited to
the analysis of non-linear structures, because no superposition is
invoked. A simplified modal response spectrum analysis has been performed;
this type of analysis can be used strictly speaking only to structures
whose response is not significantly affected by contributions from higher
modes of vibration.
In the analysis the X-axis coincides
with the longitudinal axis of the bridge, the Z-axis is in the transversal
direction and the Y-axis is vertical.
For each direction the mode of vibration
considered is the mode corresponding to the maximum participation factor.
Moreover the seismic actions of each
direction have been applied contemporarily on the F.E. model with the
combination factors according to Eurocode 8.
The following figures show the modes of
vibrations used for the seismic analysis.
Mode of vibration along Z
(mode of vibration no. 1)

Assonometric view

Plan view
The first mode of vibration is translational, its
eigenfrequency is 6.88 Hz and the participation mass is equal to 53 % of
the total mass.
Mode of vibration along X
(mode of vibration no. 2)

Assonometric view

Front view
The second eigenfrequency is equal to 10.48 Hz, the
correspondent mode of vibration is anti-symmetrical in the vertical plane
and the participation mass is equal to 25 % of the total mass.
Mode of vibration along Y (mode
of vibration no. 4)
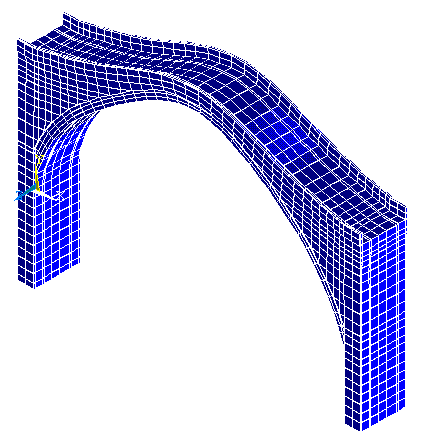
Assonometric view
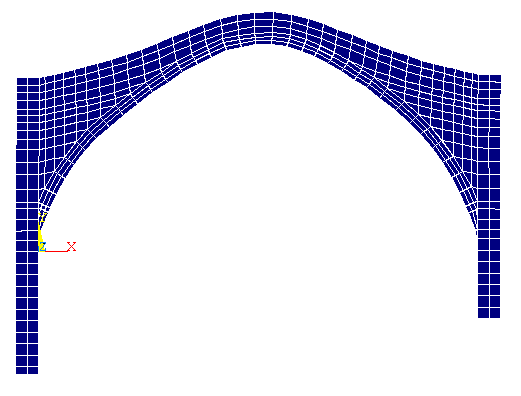
Front view
The fourth eigenfrequency is 14.68 Hz and the
correspondent participation mass is 37 % of the total mass.
The above shown modes of vibrations are uncoupled; the
modal mass is high in one direction and small in the other two directions.
In the analysis under the seismic actions, in safety
the total mass of the structure has been given to each of the above shown
modes of vibration.
The effects of the earthquake have been determined
applying statically equivalent loads Fi in each node,
proportional to the nodal mass, in the direction parallel to the
considered seismic action.
The forces have been determined with the following
formula taken from Eurocode 8:
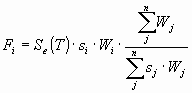 . .
where:
- Se(T)
ordinate of the design spectrum,
- Wi , WJ
weights of masses mi, mj,
- si , sJ
displacements of masses mi,
mj in the fundamental mode shape.
The weights have been computed with the following
formula:
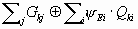 , ,
where
- Gki
characteristic value of the permanent
loads,
- Qki
characteristic value of the variable loads,
- y Ei
reduction factors of
the variable loads Qki.
Once the modes of vibration have been individualised,
the response spectrum was defined.
The horizontal seismic action is described by two
orthogonal components considered as independent and represented by the
same response spectrum.
The vertical component of the seismic action is
represented by the response spectrum as defined for the horizontal seismic
action, but with the ordinates reduced as follows:
- for vibration periods T smaller than 0,15 s the ordinates are
multiplied by factor of 0,7
- for vibration periods T greater than 0,50 s the ordinates are
multiplied by a factor of 0,50
- for vibration periods T between 0,15 s and 0,50 s a linear
interpolation is used.
The elastic response spectrum Se(T)
normalised with respect to the ground acceleration a
g is defined by the following expressions:
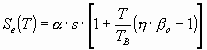
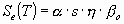
- for TC £ T £
TD

- for TD £ T
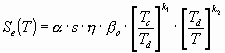
where
- Se(T)
ordinate of the elastic response spectrum,
- T
the vibration period of the mode shape considered,
- a
ratio between the peak acceleration
of the ground and the gravity acceleration g (a
= a g / g).
In particular the Stari bridge is located in a high
seismic region; a gsh
b o= 0.35 where:
b o
spectral acceleration amplification factor for 5% viscous damping,
- h damping correction factor with
reference value h = 1 for 5% viscous
damping for the masonry the Eurocode gives a viscous damping x
= 8%, which implies h = 0.84,
- TB
and TC limits of the constant
spectral acceleration branch,
- TD value defining the beginning of the constant
displacement range of the spectrum,
- k1
and k2 exponents which influence
the shape of the spectrum for a vibration period greater than TC,
TD respectively,
N.B. The behaviour factor q is not used,
because the performed analysis is non-linear.
The other coefficients are defined on the basis of the
seismic-geological characteristics of the ground.
The bridge is located in a region classifiable as class
A:
|
Class |
S |
b o |
k1 |
K2 |
TB (sec) |
TC (sec) |
TD (sec) |
|
A |
1 |
2.5 |
1.0 |
2.0 |
0.10 |
0.40 |
3.0 |
|
B |
1 |
2.5 |
1.0 |
2.0 |
0.15 |
0.60 |
3.0 |
|
C |
0.9 |
2.5 |
1.0 |
2.0 |
0.20 |
0.80 |
3.0 |
The final design spectrum is the following:
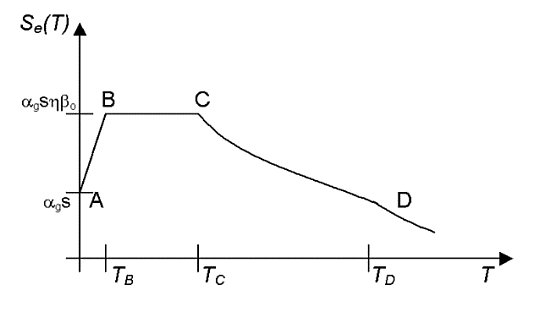
where T is the vibration period of the mode shape
considered and the characteristic points of the diagram are:
- A with Se(T)= 0.17 and TA=0 sec,
- B with Se(T)= 0.35 and TB=0.10
sec,
- C with Se(T)= 0.35 and TC=0.40
sec,
The spectral ordinates, relative to each direction,
are:
T = 0.15 sec Þ Se(T) =
0.35,
T = 0.10 sec Þ Se(T) =
0.35,
T = 0.07 sec Þ Se(T)=
0.30 * 70% = 0.21.
The horizontal and vertical seismic
forces to be applied in each node of the structure have been calculated
using the code "Matlab", elaborating some output files of the
code "Ansys".
The expression of the seismic forces is:
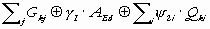 . .
Combination of the seismic forces
The seismic actions along the three directions X, Y and
Z have been combined together, as prescribed by the Eurocode (see the
following table).
| xxx |
Along X |
Along Y |
Along Z |
|
Prevailing earthquake along X |
1.00 |
0.30 |
0.30 |
|
Prevailing earthquake along Y |
0.30 |
1.00 |
0.30 |
|
Prevailing earthquake along Z |
0.30 |
0.30 |
1.00 |
The seismic actions have been combined
with the other actions according to Eurocode 8:
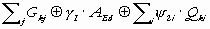
where:
- Gki
characteristic value of the permanent
loads,
- g I importance
factor of the structure,
- AEd design value of the seismic forces,
- Qki
characteristic value of the variable loads,
- y 2i
reduction factors of
the variable loads (all zero)
|