back   back to menu
STRUCTURAL DESIGN - PART 07

English english language

12. Load combination 3B
  • 1,35 permanent loads + 1,35 traffic loads on the whole bridge
  • maximum value of the elasticity modulus for the arch and minimum value for the other structural elements

fig. 25 - deformed configuration (load combination 3B)

fig. 26 - principal stresses S1 (load combination 3B)

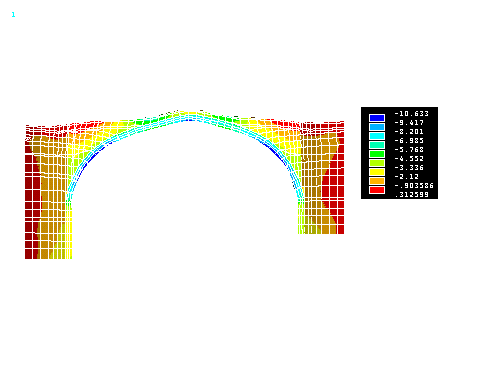
fig. 27 - principal stresses S3 (in kg/cm2) (load combination 3B)

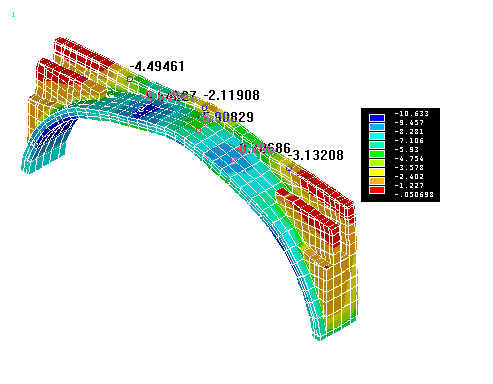
fig. 28 - principal stresses S3 (in kg/cm2) (load combination 3B)

fig. 29 - principal stresses S3 in the arch (in kg/cm2)

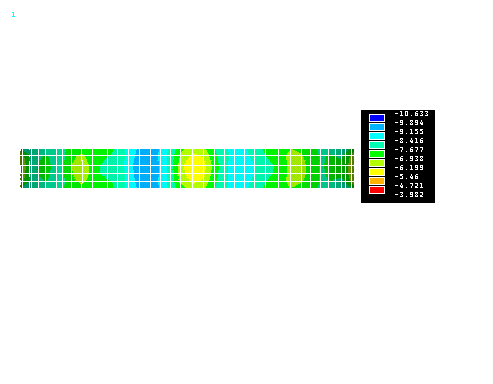
fig. 30 - principal stresses S3 (in kg/cm2) at the arch extrados (load combination 3B)

fig. 31 - principal stresses S3 (in kg/cm2) at the arch intrados (load combination 3B)

The main differences obtained between the two analyses 3A and 3B are represented by the following variations of the stresses:

  • the maximum compressive stress at the extrados of the arch in the region of the crown changes from –8.66 kg / cm2 (analysis 3A) to –9.64 kg / cm2 (analysis 3B), exhibiting a percentage variation of + 11.32 %
  • the maximum compressive stress in the spandrel decreases in the analysis 3B to the value of –7.17 kg / cm2 (with a percentage variation of - 24 % with respect to the analysis 3A)

These variations show how much the model is sensible to the variation of the elasticity modulus of the masonry:

an increase of the elasticity modulus of the arch from 8000 MPa to 10000 (percentage variation of +25 %) and the simultaneous reduction of the elasticity modulus of the other elements (- 40 %) implies an increase of the stresses in the arch of about 10 % and a reduction of about 25 % in the spandrels.

These results highlight the importance of correctly evaluating the material characteristics to get reliable results. Anyway the range of variation considered for the elasticity modulus is so large that covers the uncertainties on the real value of the elasticity modulus. Therefore, the results obtained can be considered as upper limits for the compressive stresses in the masonry produced by the permanent loads and the live loads.

CREDITS:

Intellectual property of this report and of the design drawings is owned by the University of Florence - Department of Civil Engineering

author of the text: Prof.Eng. Andrea Vignoli – other contributes have been mentioned in related paragraphs

© - General Engineering Workgroup -

SOURCE:

Final Design Report
back   back to menu
ani.gif (16635 bytes)
GENERAL ENGINEERING - P.zzale Donatello 4 - 50132 Firenze - Italy - ph. +39 055 2345256 - fax. +39 055 2476074