In the second stage the Ansys calculation code was adopted. This programme enables to perform non-linear analyses of the structure. The F.E. model has been created with the available data.

I. Modelling of non-linear material behaviour:

The brittle behaviour of masonry has been modelled through an appropriate failure criterion, here defined by means of only two material parameters f_t (uniaxial tensile strength) and f_c (uniaxial compressive strength); cross section of the assumed failure surface will be defined with a cyclic symmetry about each 120° sector of the deviatoric plane. Both cracking and crushing failure modes have been accounted for. The presence of a crack at an integration point has been represented through modification of the stress-strain relations by introducing a plane of weakness in a direction normal to the crack face. Also, a shear transfer coefficient ß has been introduced (depending on the crack status. open -ß_t- or re-closed -ß_c-), representing a shear strength reduction factor for those subsequent loads inducing sliding (shear) across the crack face.

II. Rate independent plasticity: Frictional and dilating behaviour of masonry

In order to reduce the number of the parameters employed to represents the non-linear behaviour of masonry; a Drucker-Prager perfectly plastic criterion has been employed in the model, avoiding the need for definition of a hardening rule. In this way cohesion c and angle of internal friction f has been assumed, as the only two material parameters required defining the yield surface. A non-associated flow rule has been adopted for determining the direction of plastic straining, which has been calculated assuming the angle of dilitancy n instead of the angle of internal friction. The dilitancy (which represents a third material parameter) controls both the volumetric expansion during the plastic straining and its deviation from the associated flow rule, the correct setting of the dilitancy value, moreover, permits to define the relevance of the frictional behaviour of the material, as n = 0° signifies a pure frictional behaviour with no volume change during the plastic flow, while n = f indicates a purely dilating or perfectly plastic material with zero friction and the validity of the flow rule. Several ways are possible in order of representing relationships between f and n (see f. i. Bishop (1950), Rowe (1962) and Davis (1968)), focusing the major attention on the physical meaning of the parameters, as represented in Fig. A, where the trace of the yield function is depicted in a meridian plane in the t - s stress space.

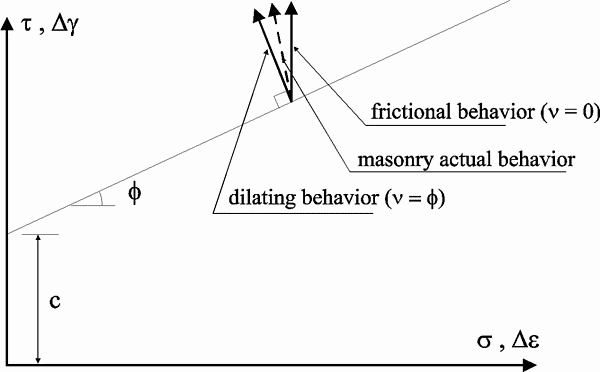
fig. A - Frictional and dilating behaviour: flow rule for masonry material

III. Failure surface

The failure criterion has been adopted (William and Warnke (1975)), initially defined for concrete, accounts for both cracking and crushing failure modes trough a smeared model. Despite the need for five constants in order to define the criterion, in most practical cases (thereby when the hydrostatic stress is limited by f_c,) the adopted failure surface has been specified by means of the only two constants: f_t and f_c (respectively the uniaxial tensile and compressive strength). The failure surface that has been adopted is depicted in Fig. B.

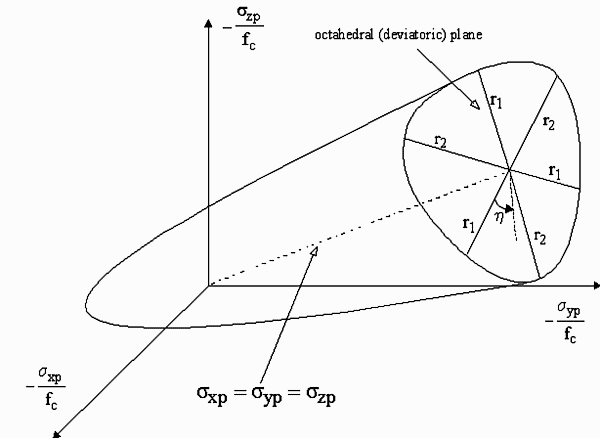
fig. B - Failure surface

IV. References

ANSYS (1993) Revision 5.0A, Swanson Analysis System, Inc., Houston.

Bishop, AW, (1950) Discussion on measurement of the shear strength of soils. Geotechnique, Vol. 2, No. 1, pp. 113 -116.

Davis, E.H., (1968) Theories of plasticity and the failure of soil masses, in I.K. Lee (Editor), Soil mechanics: selected topics. Butterworth, London, pp. 341-380.

Rowe, P.W., (1962) The stress-dilitancy relation for static equilibrium of an assembly of particles in contact. Proc. R. Soc. London, Ser. A, 269, pp. 500-527.

William, K.J., Warnke, E.D., (1975) Constitutive model for the triaxial behaviour of concrete , Proc. Int. Ass. for Bridge and Struct. Engng., Vol. 19, ISMES, Bergamo, pp. 174-186.

First a linear analysis was performed, obtaining a thrust line similar to the one found before in the F.E. model of the arch alone, but less eccentric.

The tensile stresses were very limited because the solid modelling allowed for taking into account also the contribution of the other elements (spandrels, slab) to the bearing mechanism. The solid model provided a better description of the stress patterns within each section than the beam model. A non-symmetrical stress pattern has been obtained, which confirms that the bridge has acquired a non symmetrical configuration due to the settlements of its foundations and the settlement of the centering.

The linear analyses were performed taking into account a maximum tensile stress of 0,5 kg/cm² in the masonry. This means that in the regions were the tensile stresses were over this limit, the finite elements were separated to simulate the formation of cracks. With this operation the linear analyses performed allow for taking into account, with a good approximation, the non-linear behaviour of the masonry.

The analyses under the permanent loads, the live loads and the thermal actions were performed in the linear field, but the model connectivity was modified according to the stress pattern present in the model: in the regions where the stresses were higher than the prefixed limit of 0,5 kg/cm² the elements were disconnected or the external restraints were removed. Therefore, for each load combinations, different mesh disconnections and restraint conditions were defined.

On the contrary non-linear analyses were performed under the flood loads and the earthquake actions.

For these analyses a different F.E. model was created, reducing the elements of the abutments and increasing the limit traction to improve the convergence of the non-linear analyses. The results obtained show that the maximum tensile stresses do not concern the main arch.

Intellectual property of this report and of the design drawings is owned by the University of Florence - Department of Civil Engineering

author of the text: Prof.Eng. Andrea Vignoli – other contributes have been mentioned in related paragraphs